ครั้งนี้จะมาลองทำ A/B Testing ตาม 2 ท่านนี้ Mobile Games A/B Testing และ A/B Testing: Step by Step & Hypothesis Testing แน่นอนว่าผลลัพธ์หรือวิธีการคิดอาจจะเหมือนหรือแตกต่างกันออกไป จากตัวอย่างเค้าใช้ python แต่เราจะใช้ภาษา R กันบ้าง หลังจากที่วิเคราะห์โดยใช้ python กันไปแล้วในโพสต์นี้ “มาทำ AB Testing ใน python กัน” นะครับ
Cookie Cats เป็นเกมที่เป็นที่นิยม ถูกพัฒนาโดย Tactile Entertainment เป็น puzzle game ที่ใช้การลากเชื่อมต่อบล็อกสีเดียวกันให้ได้แต้มมากที่สุดเพื่อชนะและผ่านด่านเลเวล มีแมวเป็นตัวละครหลัก

เมื่อเล่นเกมไปเรื่อยๆ จะเจอกับ gate ที่บังคับให้ผู้เล่นต้องรอสักพักก่อนที่จะสามารถเล่นต่อหรือซื้อสินค้าภายในแอปได้ นอกจากจะกระตุ้นให้เกิดการซื้อของในแอปแล้ว gate เหล่านี้ยังมีจุดประสงค์สำคัญในการบังคับให้ผู้เล่นหยุดพักจากการเล่นเกม ซึ่งหวังว่าจะทำให้ผู้เล่นสนุกกับเกมมากขึ้น และยาวนานขึ้น
แต่ gate ควรวางไว้ตรงไหน? เดิมที gate แรกถูกวางไว้ที่เลเวล 30, ในโปรเจกต์นี้ เราจะวิเคราะห์การทดสอบ AB จากการย้าย gate จากเลเวล 30 ไปยังเลเวล 40 จะมีผลกระทบต่อ:
- จำนวนรอบการเล่น
- การรักษาผู้เล่น (ว่าจะยังคงเล่นเกมนี้ต่อไป)
Load the AB-test data
# install.packages('dplyr', 'readr', 'ggplot2', 'nortest')
# load library
library(dplyr)
library(readr)
library(ggplot2)
library(nortest)
library(boot)
library(tidyr)
# import data csv
file_name <- "RefFiles/cookie_cats.csv"
df <- tibble(data.frame(read_csv(file = file_name)))
head(df, 5)
summary(df)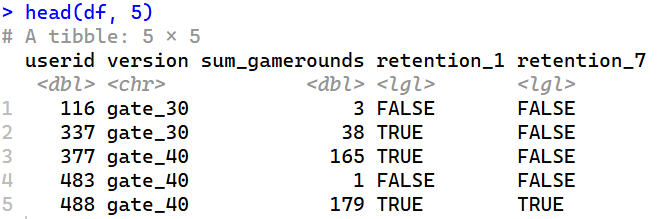
ข้อมูลมากจากผู้เล่น 90,189 คน ที่ติดตั้งเกมนี้และอยู่ในช่วงที่กำลังรันโปรเจ็ค AB-test นี้อยู่ มีตัวแปรดังนี้:
userid– หมายเลขผู้เล่นในเกม (1 ผู้เล่น : 1 หมายเลข)version– กลุ่มที่แสดงว่าผู้เล่นถูก ‘สุ่ม’ ให้อยู่ในกลุ่มใด- โดยที่กลุ่มควบคุม (control group) คือ
gate_30– มีประตูดักที่เลเวล 30 - และกลุ่มทดสอบ (test group) คือ
gate_40– มีประตูดักที่เลเวล 40
- โดยที่กลุ่มควบคุม (control group) คือ
sum_gamerounds– จำนวนการเล่นเกม(รอบ)ในสัปดาห์แรกหลังจากติดตั้งเกมแล้วretention_1– ผู้เล่นกลับมาเล่นอีกครั้งภายใน 1 วันหลังติดตั้งใช่มั้ย?— ผู้เล่นกลับมาเล่นหลังจากติดตั้งไปแล้ว 1 วันหรือไม่?retention_7– ผู้เล่นกลับมาเล่นอีกครั้งภายใน 7 วันหลังติดตั้งใช่มั้ย?—ผู้เล่นกลับมาเล่นหลังจากติดตั้งไปแล้ว 7 วันหรือไม่?- เมื่อผู้เล่นติดตั้งเกม พวกเขาจะถูก ‘สุ่ม’ ให้อยู่ในกลุ่ม
gate_30หรือgate_40
Check missing values
ปกติเมื่อเราใช้ summary() ก็จะบอกจำนวน NA’s ออกมาเลยครับ –แต่ในผลด้านล่างไม่มีค่าว่างครับ

แต่ก็จะมาโค้ดออกมาได้เช่นกัน
#### check missing values ####
summary(df)
# missing ของแต่ละ cols มีมั้ย? T/F
apply(df, 2, function(x) any(is.na(x)))
# missing ของแต่ละ col มีจำนวนเท่าไหร่?
colSums(is.na(df))
โอเค จะเห็นว่า dataset นี้ไม่มีข้อมูลว่าง
Count the number of players in each group
# count the number of players in each group
df %>%
group_by(version) %>%
summarise(n_row = n())
เนื่องจากผู้เล่นถูกสู่มให้อยู่ในแต่ละกลุ่ม จำนวนผู้เล่นในแต่ละกลุ่มจึงใกล้เคียงกัน ซึ่งดีแล้ว
Analyzing Player Behavior
เราจะสร้าง boxplot เพื่อแสดงภาพการกระจายของ sum_gamerounds ซึ่งจะทำให้เรามีความคิดคร่าวๆ ว่าผู้เล่นเล่นไปกี่รอบในสัปดาห์แรกหลังจากติดตั้งเกม
# boxplot
library(ggplot2)
df %>%
ggplot(aes(sum_gamerounds)) +
geom_boxplot()
fivenum(df$sum_gamerounds) # ดู Q0-Q4 คร่าวๆ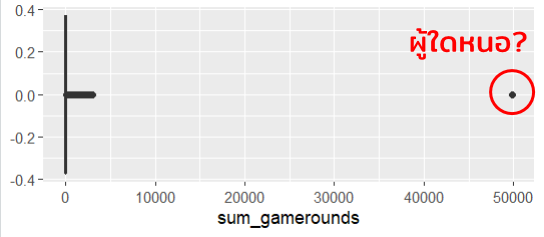
เห็นได้ชัดว่ามีค่าผิดปกติ ผู้เล่นคนนี้เล่นเกมไปประมาณ 50,000 รอบในสัปดาห์แรก! (หรือใช้ fivenum() เช็คก็ได้ ผู้เล่นคนนั้นเล่นไปถึง 49,854 รอบใน 1 สัปดาห์) เนื่องจากค่าผิดปกตินี้ boxplot นี้จึงมีความเบ้ อย่างมาก และไม่ได้เป็นตัวแทนที่ดีเพื่อที่จะเรียนรู้เกี่ยวกับพฤติกรรมของผู้เล่นส่วนใหญ่

จากผลลัพธ์จะเห็นว่า จำนวนผู้เล่น 50% เล่นเกมน้อยกว่า 16 รอบในสัปดาห์แรกหลังจากการติดตั้ง (50% ย้อนกลับไปทางซ้าย) และผู้เล่น 75% เล่นน้อยกว่า 51 รอบ — มาลองนับจำนวนครั้งการเล่นกัน
# group by gamerounds
df %>%
group_by(sum_gamerounds) %>%
summarise(n_row = n()) %>%
head(10)
df %>%
group_by(sum_gamerounds) %>%
summarise(n_row = n()) %>%
tail(10)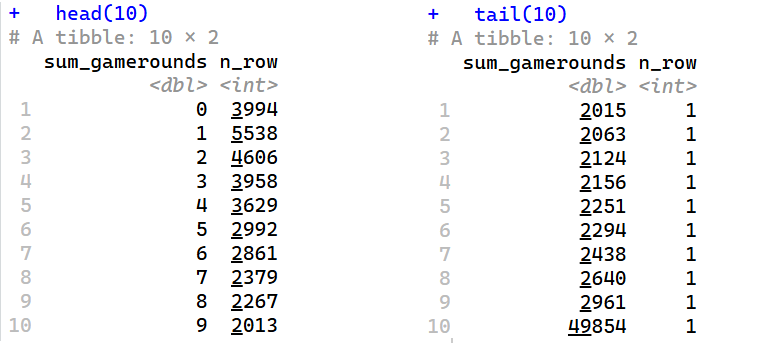
มีผู้เล่นเกือบ 4,000 คนที่ไม่ได้เล่นเกมเลยซักรอบหลังจากติดตั้ง สาเหตุ “อาจ” เป็นเพราะ..
- เค้าดาวน์โหลดเกมใหม่หลายเกมพร้อมกัน และรู้สึกสนใจเกมอื่นๆ มากกว่า
- เค้าเปิดแอปแต่ไม่ชอบดีไซน์/อินเทอร์เฟซ/เพลงประกอบ จึงเลิกเล่นเกมนี้ไปก่อนที่จะเริ่มเล่น
- เค้ายังไม่ได้เล่นเกมจริงๆ
- และอื่นๆ
อีกหนึ่ง stat ที่น่าสนใจคือ ผู้เล่นมากกว่า 14,000 คน ที่เล่นน้อยกว่าสามรอบ (3,994 + 5,538 + 4,606 = 14,138) เหตุผลที่ไม่เล่นต่อก็ “อาจจะ” เป็น :
- เกมไม่จอย ไม่สนุก (อาจเป็นเหตุผลหลัก)
- แนวการเล่นเกมต่างจากที่คาดหวังไว้ ไม่ตรงปก
- เกมง่ายเกินไป จนเบื่อ
- และเหตุผลอื่นๆ
เป็นเรื่องที่ดี ที่จะทำความเข้าใจว่าทำไมผู้เล่นจำนวนมากจึงเลิกเล่นเกมตั้งแต่ช่วงแรกๆ บ.ผู้พัฒนาควรจะรวบรวมความคิดเห็น feedback จากผู้เล่น เพื่อพัฒนาต่อด้วย
ทั้งนี้ขอจัดการ outlier คนนั้นออกไปก่อนนะครับ ด้วยโค้ดนี้
# outlier
max_outlier <- max(df$sum_gamerounds)
df <- df %>% filter(sum_gamerounds < max_outlier)
summary(df)
# boxplot
df %>%
ggplot(aes(sum_gamerounds)) +
geom_boxplot()
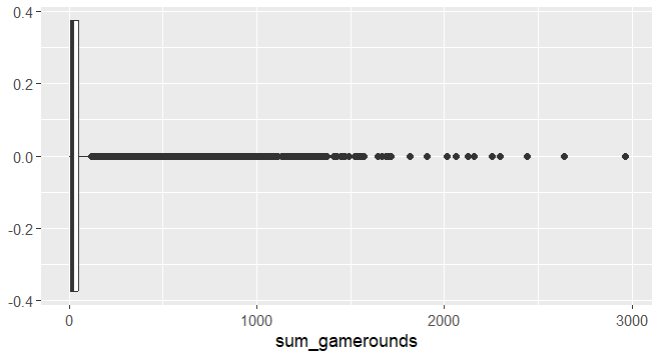
ต่อไปเป็นการพล็อตการกระจายของผู้เล่นที่เล่นเกม 0 ถึง 100 รอบในสัปดาห์แรกที่เล่นเกม
plot_df <- df %>%
group_by(sum_gamerounds) %>%
summarise(n_row = n())
plot_df <- plot_df[1:100, ]
plot_df %>%
ggplot(aes(sum_gamerounds, n_row)) +
geom_line(color = "navy") 
การกระจายตัวมีความเบ้(ขวา)อย่างมาก โดยมีหางยาวอยู่ทางด้านขวา มีผู้เล่นจำนวนมากเล่นน้อยกว่า 25 รอบและออกจากเกมไป 😿 — ที่นี้มาดู การกระจายตัวของทั้ง 2 กลุ่มกันบ้าง
# boxplot by version
df %>%
ggplot(aes(version, sum_gamerounds)) +
geom_boxplot()
ทดสอบจำนวนรอบการเล่น-play rounds
เราจะใช้ตัวแปร sum_gamerounds (จำนวนการเล่นเกม(รอบ)ในสัปดาห์แรกหลังจากติดตั้งเกมแล้ว) ในการทดสอบครั้งนี้ว่า “การเปลี่ยน gate จากเลเวล 30 เป็น 40 นั้น ส่งผลต่อจำนวนการกลับเข้ามาเล่นเกมหรือไม่ใน 1 สัปดาห์” ซึ่งการเปิดเข้ามาเล่นเกมกี่ครั้งต่อวัน ก็บอกได้ว่าเกมสามารถแทรกเข้าสู่กิจวัตรประจำวันของผู้เล่นได้ดีแค่ไหน
Lilliefors Test
การทดสอบ Normality จึงต้องทำเป็น ขั้นตอนแรกๆ ในส่วนของการตรวจสอบสมมติฐาน (Assumption Checking) ก่อนการทดสอบสมมติฐานหลัก เพราะ มันคือตัวกำหนดทิศทาง (Roadmap) ของการวิเคราะห์สถิติ ผลลัพธ์จากการทดสอบ Normality เป็นตัวกำหนดว่าควรเลือกใช้เครื่องมือ/วิธีการทางสถิติใดในการเปรียบเทียบผลลัพธ์ A/B Testing:
- หากเป็นปกติ → เลือกใช้ T-Test (Parametric)
- หากไม่เป็นปกติ → เลือกใช้ Mann-Whitney U Test (Non-Parametric)
เนื่องจาก Shapiro-Wilk Test มีความอ่อนไหวสูงมากเมื่อ N มีขนาดใหญ่ — จึงเลือกใช้ Lilliefors Test เนื่องจากเป็นข้อมูลที่มีขนาดใหญ่ (N > 50)

ต้องทำการทดสอบ Normality แยกกัน สำหรับตัวแปร sum_gamerounds ในแต่ละกลุ่มย่อย (gate_30 และ gate_40) และต่อด้วย Density plot เพื่อดูการแจกแจงด้วยตาไปด้วย
โดย Lilliefors Test มีสมมติฐานคือ
- Null Hypothesis (H0): The data is normally distributed
- Alternative Hypothesis (HA): The data is not normally distributed
- โดยที่ p-value > 0.05 – Fail to reject H0
- และหาก p-value <= 0.05 – Reject H0
#### Check normality ####
# ติดตั้งแพ็กเกจ nortest หากยังไม่มี
# install.packages("nortest")
library(nortest)
# ทำการทดสอบ Lilliefors
# แยกข้อมูลกลุ่ม gate_30
group_30 <- df[df$version == "gate_30", "sum_gamerounds"]
# ทำการทดสอบ Lilliefors
lillie_30 <- lillie.test(group_30$sum_gamerounds)
lillie_30
if (lillie_30$p.value <= 0.05 ){
print("Reject H0 :: It's not normally distributed")
print("Use: Mann-Whitney U Test (Non-Parametric)")
} else {
print("Fail to reject H0 :: It's normally distributed")
print("Use: T-Test (Parametric))")
}
# Create the overlaid density plot
ggplot(group_30, aes(x = sum_gamerounds)) +
geom_density(alpha = 0.5) + # Use transparency for better visualization
labs(title = "Density Plot of sum_gamerounds in group_30",
x = "Value",
y = "Density") +
theme_minimal()
# แยกข้อมูลกลุ่ม gate_40
group_40 <- df[df$version == "gate_40", "sum_gamerounds"]
# ทำการทดสอบ Lilliefors
lillie_40 <- lillie.test(group_40$sum_gamerounds)
lillie_40
if (lillie_40$p.value <= 0.05 ){
print("Reject H0 :: It's not normally distributed")
print("Use: Mann-Whitney U Test (Non-Parametric)")
} else {
print("Fail to reject H0 :: It's normally distributed")
print("Use: T-Test (Parametric))")
}
# Create the overlaid density plot
ggplot(group_40, aes(x = sum_gamerounds)) +
geom_density(alpha = 0.5) + # Use transparency for better visualization
labs(title = "Density Plot of sum_gamerounds in group_40",
x = "Value",
y = "Density") +
theme_minimal()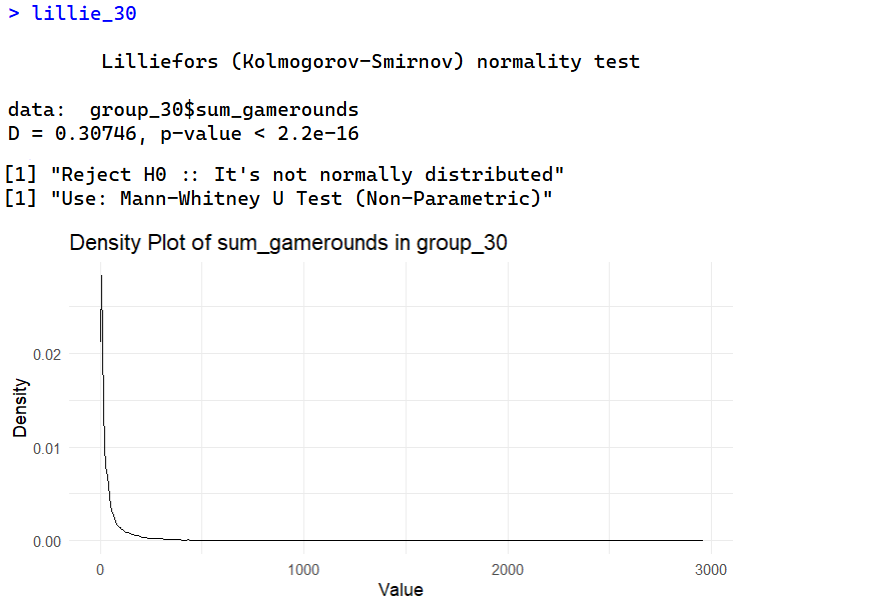
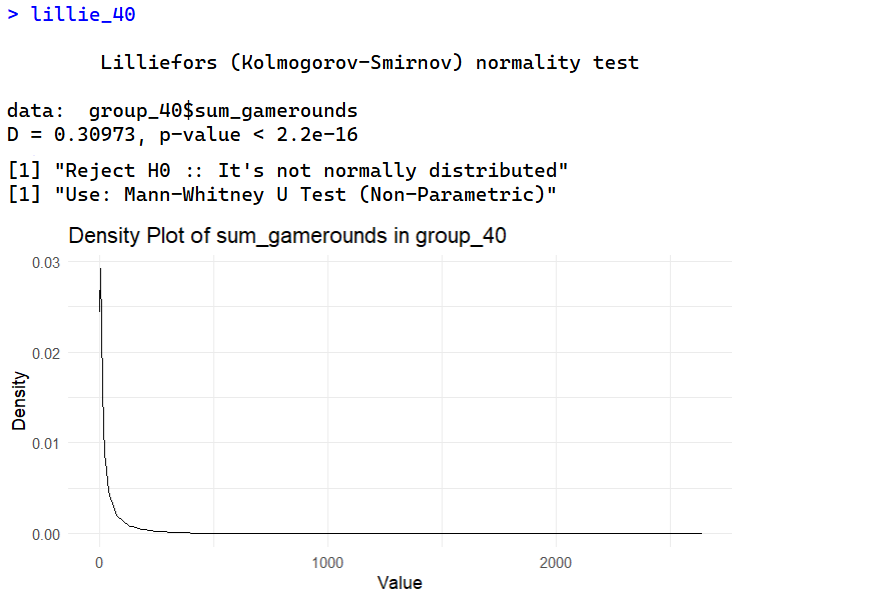
ทั้ง 2 กลุ่มมีการแจงแจงของ sum_gamerounds ที่ไม่ปกติ ทำให้ขั้นตอนต่อไปเลือกใช้ Mann-Whitney U Test (Non-Parametric) ในการทดสอบเปรียบเทียบผลลัพธ์ A/B Testing ของจำนวนรอบเกมที่เล่น sum_gamerounds เพื่อให้มั่นใจในความถูกต้องทางสถิติ (Statistical Robustness) ที่จะเปรียบเทียบค่ามัธยฐาน (Median) ของสองกลุ่มที่เป็นอิสระต่อกัน
Mann-Whitney U Test
โอเคเรารู้แล้วว่าทั้ง 2 กลุ่มไม่ Normal distributed แต่การที่แจกแจงที่ไม่ปกตินั้นของทั้งคู่มันแตกต่างกันจริงหรือไม่? Mann-Whitney U Test เป็นการทดสอบสมมติฐานเพื่อเปรียบเทียบว่าการแจกแจงของประชากรทั้งสองกลุ่มแตกต่างกันอย่างมีนัยสำคัญหรือไม่
- Null Hypothesis (H0) การแจกแจงของ
sum_gameroundsของกลุ่มgate_30และgate_40ไม่แตกต่างกัน (หรือมีค่ามัธยฐานเท่ากัน) - Alternative Hypothesis (HA) การแจกแจงของ
sum_gameroundsของกลุ่มgate_30และgate_40แตกต่างกัน (หรือมีค่ามัธยฐานไม่เท่ากัน)
โดยที่
- ถ้า p-value ≤ 0.05 เราจะ Reject H0 — มีหลักฐานทางสถิติที่ชัดเจนว่าการแจกแจงของ
sum_gameroundsระหว่างสองกลุ่ม แตกต่างกันอย่างมีนัยสำคัญ (นั่นคือ มีกลุ่มหนึ่งเล่นเกมมากกว่าอีกกลุ่ม) - p-value > 0.05 ก็ Fail to reject H0 — ไม่มีหลักฐานทางสถิติที่ชัดเจนว่าการแจกแจงของ
sum_gameroundsระหว่างสองกลุ่ม แตกต่างกันอย่างมีนัยสำคัญ (ผลการเปลี่ยนแปลงตำแหน่ง Gate ไม่มีผล ต่อจำนวนรอบเกมที่เล่น)
mann_whitney_result <- wilcox.test(sum_gamerounds ~ version,
data = df,
conf.int = TRUE)
# เพิ่ม conf.int = TRUE เพื่อให้คำนวณช่วงความเชื่อมั่น (Optional)
# แสดงผลลัพธ์
mann_whitney_result
if (mann_whitney_result$p.value <= 0.05 ){
print("Reject H0")
print("There are statistically significant difference between two groups")
} else {
print("Fail to reject H0")
print("There are 'not' statistically significant difference between two groups")
}
จะได้ผล p-value = 0.05089 ทำให้ได้ข้อสรุปที่ว่า ไม่มีหลักฐานทางสถิติที่ชัดเจนว่าการแจกแจงของ sum_gamerounds ระหว่างสองกลุ่ม แตกต่างกันอย่างมีนัยสำคัญ (ผลการเปลี่ยนแปลงตำแหน่ง Gate ไม่มีผล ต่อจำนวนรอบเกมที่เล่น)
เนื่องจากการทดสอบนี้เป็นการเปรียบเทียบค่า มัธยฐาน (Median) แทนที่จะเป็นค่าเฉลี่ย (Mean) จึงขอตรวจสอบเพิ่มอีกนิดนึง — ค่ามัธยฐาน (Median): ใช้ฟังก์ชัน aggregate() หรือ tapply() เพื่อคำนวณค่ามัธยฐานของ sum_gamerounds ในแต่ละกลุ่ม เพื่อดูว่ากลุ่มใดมีค่าสูงกว่า
median_rounds <- aggregate(sum_gamerounds ~ version, data = df, FUN = median)
median_rounds
โอเคเข้าใจได้ 😏 การย้าย gate จากเลเวล 30 ไปเลเวล 40 ทำให้จำนวนรอบการเล่นเกมต่างกันเพียง 1 รอบเอง แต่…
- จะเห็นว่า p-value ที่ได้นั้นคาบเกี่ยวกับ alpha 0.05 ที่เราตั้งไว้แบบหวุดหวิดมากจึงทำให้สรุปผลได้ว่า การเปลี่ยนแปลงตำแหน่ง Gate ไม่มีผล ต่อจำนวนรอบเกมที่เล่น — เพราะเราไม่มีหลักฐานเพียงพอที่จะบอกได้ว่าการย้าย Gate มีผลต่อจำนวนรอบเกมที่เล่นในเชิงสถิติ
- แต่ในทางธุรกิจที่มีข้อมูลมหาศาล (N ~ 40,000 ผู้เล่นต่อกลุ่ม) ความแตกต่างเพียงเล็กน้อยนี้ก็อาจจะมีผลต่อ มิติทางธุรกิจ ได้ด้วย
- คำถามทางธุรกิจ: แม้ความแตกต่างเพียง 1 รอบจะ “ดูเหมือน” น้อย แต่ในมุมมองของเกมที่มีผู้เล่นเป็นล้านคน การสูญเสียผู้เล่นที่เลิกเล่นเร็วขึ้น 1 รอบ (16 เทียบกับ 17) อาจส่งผลกระทบมหาศาลต่อ Retention Rate และ Lifetime Value (LTV) ของผู้เล่นในระยะยาว
- เนื่องจากไม่มีนัยสำคัญทางสถิติ และ Gate 40 มีค่ามัธยฐานต่ำกว่า (16 vs 17) การตัดสินใจที่ปลอดภัยที่สุดและถูกหลักการคือ คง Gate ไว้ที่ Level 30 (กลุ่มควบคุม)
- การตัดสินใจนี้ยังสอดคล้องกับหลักการ A/B Test ที่ว่า: หากผลลัพธ์ไม่มีนัยสำคัญทางสถิติ ห้ามนำเวอร์ชันใหม่มาใช้ โดยเฉพาะเมื่อเวอร์ชันใหม่ (Gate 40) มีแนวโน้มที่ตัวชี้วัด (จำนวนรอบเกม) จะลดลง
ทดสอบการคงอยู่ – Retention
Comparing 1-day Retention
จากตารางข้างต้น จะเห็นว่าผู้เล่นบางคนติดตั้งเกมแล้วแต่กลับไม่เคยเล่นเลย บางคนเล่นแค่สองสามรอบในสัปดาห์แรก และบางคนก็เล่นยาว! สิ่งที่เราต้องการคือให้ผู้เล่นชอบเกมและเล่นเกมอยู่เรื่อยๆ
ตัวชี้วัดทั่วไปที่ใช้วัดความสนุกและความน่าสนใจของเกม คือ 1-day retention ซึ่งก็คือเปอร์เซ็นต์ของผู้เล่นที่กลับมาเล่นเกมอีกครั้งหลังจากติดตั้งเกมไปแล้ว 1 วัน — ยิ่ง 1-day retention สูงเท่าไหร่ ก็ยิ่งทำให้การรักษาผู้เล่นและสร้างฐานผู้เล่นขนาดใหญ่ไว้ได้ง่ายขึ้นเท่านั้น
# Comparing 1-day Retention
sum(df$retention_1) / nrow(df)
# sum(df$retention_1) # ผลรวมของ logical; True = 1, False = 0 จำนวนที่ผู้เล่นที่กลับมาใน 1 วัน
# nrow(df) # นับจำนวนแถว นั่นก็คือ จำนวนผู้เล่นทั้งหมด
# สูตรคุ้นๆ มันคือ mean() นั่นเอง ดังนั้นโค้ดแบบนี้ก็ได้
mean(df$retention_1)
ในภาพรวมจะเห็นว่า มีผู้เล่นน้อยกว่าครึ่ง (45%) ที่กลับมาเล่นหลังจากติดตั้งเกมไปแล้วหนึ่งวัน (นั่นคือ 55% ไม่ได้กลับมาเล่นหลังติดตั้งไปแล้ว 1 วัน) มาดูกันว่า 1-day retention ระหว่างกลุ่ม AB นั้นแตกต่างกันอย่างไร
# 1-day retention for each AB-group
df %>%
group_by(version) %>%
summarise(mean_grp = mean(retention_1))
จากตัวเลข 1-day retention ของกลุ่มควบคุม (test group) จะลดลงเล็กน้อยเมื่อย้ายประตูไปที่เลเวล 40 (0.442) —เมื่อเทียบกับกลุ่มควบคุม (control group) ที่ประตูอยู่ที่เลเวล 30 (0.448) การเปลี่ยนแปลงนี้แม้จะเล็กน้อย ก็อาจส่งผลกระทบอย่างมากได้ ถึงแม้จะมั่นใจในความแตกต่างของข้อมูลแล้ว
แต่เราจะมั่นใจได้แค่ไหนว่าเกตที่เลเวล 40 จะแย่ลงในอนาคต (หากเกมยังให้บริการแบบเดิมอยู่) มีวิธีที่เราสามารถประเมินความแน่นอนของตัวเลขการคงอยู่เหล่านี้ได้ (ไม่ churn ออกไปซะก่อน) ในครั้งนี้จะใช้วิธีการบูตสแตรป (bootstrapping): โดยสุ่มตัวอย่างชุดข้อมูลซ้ำๆ (พร้อมการแทนที่)
แวะโน๊ต:: bootstrapping re-sample การสุ่มโดยการใส่ข้อมูลเดิม (ที่ถูกสุ่มขึ้น) กลับลงไปอีกครั้ง เหมาะกับข้อมูลจำนวนน้อยแต่ต้องการผลการทดสอบที่ดีขึ้น
และคำนวณ 1-day retention สำหรับตัวอย่างเหล่านั้น การเปลี่ยนแปลงของ 1-day retention จะทำให้ทราบถึงความไม่แน่นอนของตัวเลขการคงอยู่ได้
# boots A group
boots_a_stat <- function(data, indices) {
# ดึงข้อมูล index ที่ Resample มา
d <- data[indices, ]
# คำนวณค่าเฉลี่ยของแต่ละกลุ่ม A
mean_A <- d %>% filter(version == "gate_30") %>% pull(retention_1) %>% mean(na.rm = TRUE)
return(mean_A)
}
boot_a <- boot(
data = df,
statistic = boots_a_stat,
R = 1000 # จำนวนครั้ง
)
boot_a
# boots B group
boots_b_stat <- function(data, indices) {
# ดึงข้อมูล index ที่ Resample มา
d <- data[indices, ]
# คำนวณค่าเฉลี่ยของแต่ละกลุ่ม B
mean_B <- d %>% filter(version == "gate_40") %>% pull(retention_1) %>% mean(na.rm = TRUE)
return(mean_B)
}
boot_b <- boot(
data = df,
statistic = boots_b_stat,
R = 1000 # จำนวนครั้ง
)
boot_b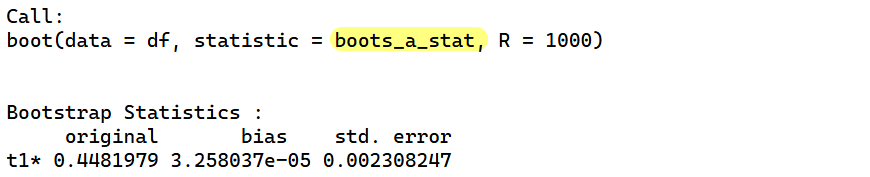
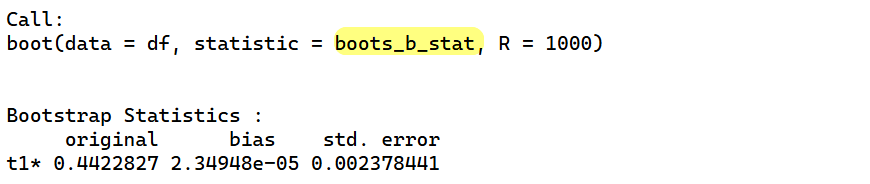
ที่นี้ ขอเอาผลลัพธ์ของ bootstrap ที่รัน 1,000 ครั้งมาพล๊อตกราฟความถี่นิดนึงจะได้แบบนี้
# plot density of mean A / B
a <- as.data.frame(boot_a[2])
b <- as.data.frame(boot_b[2])
ab_df <- bind_cols(a, b)
ab_df <- ab_df %>% select( gate_30 = t...1 , gate_40 = t...2 )
rm(a,b)
head(ab_df)
library(tidyr)
# Convert the data to long format
df_ablong <- pivot_longer(ab_df, cols = c(gate_30, gate_40), names_to = "variable", values_to = "value")
# Create the overlaid density plot
ggplot(df_ablong, aes(x = value, colour = variable)) +
geom_density(alpha = 0.5) + # Use transparency for better visualization
labs(title = "Density Plot of MeanA & MeanB",
x = "Value",
y = "Density") +
theme_minimal()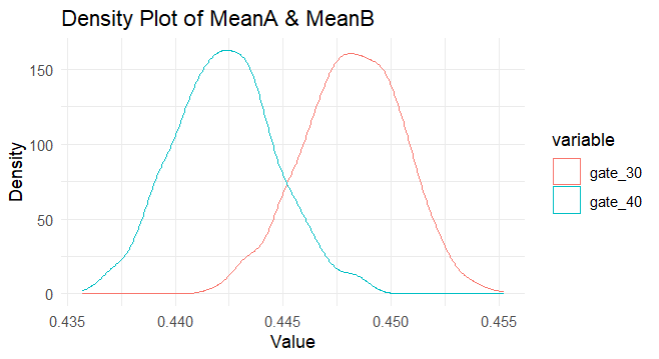
ความเป็นไปได้ของการกระจายตัวของ bootstrap 1-day retention ใน 2 กลุ่มนี้ แม้ว่าจะมีความแตกต่างเล็กน้อย จากการสุ่มทำซ้ำ 1,000 ครั้ง กลุ่ม gate_40 ก็มีอัตราการกลับมาเล่นภายใน 1 วัน น้อยกว่ากลุ่ม gate_30 (อยู่ดี—จากกราฟเส้นสีฟ้าอยู่ทางซ้าย) ลองพล็อตเปอร์เซ็นต์ความแตกต่างเพื่อดูให้ละเอียดยิ่งขึ้น
# boots Diff A-B group
boots_stat <- function(data, indices) {
# ดึงข้อมูล index ที่ Resample มา
d <- data[indices, ]
# คำนวณค่าเฉลี่ยของแต่ละกลุ่มและหาผลต่าง
mean_A <- d %>% filter(version == "gate_30") %>% pull(retention_1) %>% mean(na.rm = TRUE)
mean_B <- d %>% filter(version == "gate_40") %>% pull(retention_1) %>% mean(na.rm = TRUE)
return(((mean_B-mean_A)/mean_A)*100)
}
boot_ab <- boot(
data = df,
statistic = boots_stat,
R = 1000 # จำนวนครั้ง
)
boot_ab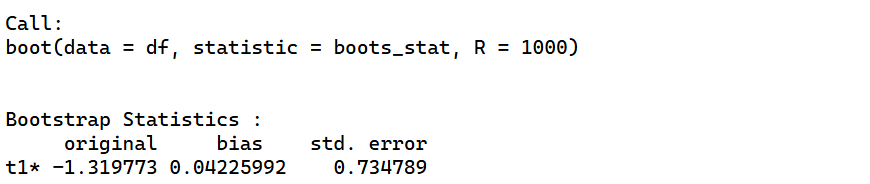
# plot density of mean A / B
a <- as.data.frame(boot_a[2])
b <- as.data.frame(boot_b[2])
dif_ab <- as.data.frame(boot_ab[2])
ab_df <- bind_cols(a, b)
ab_df <- bind_cols(ab_df, dif_ab)
ab_df <- ab_df %>% select( gate_30 = t...1 , gate_40 = t...2 , diff_ab = t...3)
rm(a, b, dif_ab)
head(ab_df, 5)
# % per diff
ggplot(ab_df, aes(x = diff_ab)) +
geom_density(alpha = 0.5) + # Use transparency for better visualization
labs(title = "Density Plot of % diff_ab",
x = "Value",
y = "Density") +
theme_minimal()
mean(ab_df$diff_ab < 0)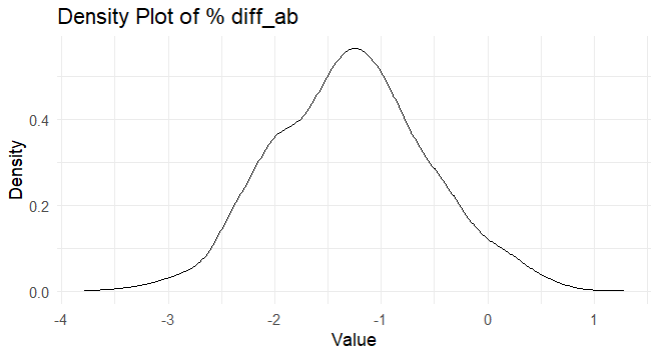
จากแผนภูมินี้ เราจะเห็นว่าเปอร์เซ็นต์ความแตกต่างที่เป็นไปได้มากที่สุดอยู่ที่ประมาณ -1% ถึง -2% และ 95% (0.951) ของการกระจายนั้นต่ำกว่า 0% ซึ่งสนับสนุนประตูที่เลเวล 30 (gate_30) —เพราะเราใช้ gate_40 เป็นตัวตั้งในการคำนวณเปอร์เซ็นต์ความแตกต่าง ถ้าผลลัพธ์เป็นบวก: คือเปอร์เซ็นต์ที่เพิ่มขึ้น, ถ้าผลลัพธ์เป็นลบ: คือเปอร์เซ็นต์ที่ลดลง

แต่อย่างว่า “อัตราการที่ผู้เล่นกลับมาเล่นอีกครั้งใน 1 วันหลังติดตั้ง” มันจะวัดการคงอยู่ของผู้เล่นได้จริงๆ หรือไม่ในชีวิตจริง —เอาจริงใน 1-2 วัน เราเล่นยังไม่ทันเบื่อเลย และหลังติดตั้งก็น่าจะมาลองเล่นอยู่แล้ว และ gate ที่วางไว้ไกลถึงเลเวล 30 หรือ 40 นั้นดูไกลเกินไปที่ 1-2 วันจะทำได้ (ยกเว้นเสียแต่ว่าผู้เล่นจะมีเวลาว่างขนาดนั้น)
ก็คือจะบอกว่ากลุ่ม A/B มีความสัมพันธ์กับความแตกต่าง -1% ถึง -2% นี้ก็จริง แต่ก็ไม่น่าจะเป็นสาเหตุ (causation) ที่ทำให้เกิดขึ้น
Comparing 7-day Retention
แต่หลังจากเล่นไปหนึ่งสัปดาห์ ผู้เล่นส่วนใหญ่น่าจะถึงเลเวล 40 แล้ว ดังนั้นจึงควรพิจารณาอัตราการคงอยู่ 7 วันด้วย
# Comparing 7-day Retention
sum(df$retention_7) / nrow(df)
mean(df$retention_7)
# 1-day retention for each AB-group
df %>%
group_by(version) %>%
summarise(mean_grp = mean(retention_7))
ผลที่ได้คือ..
- การคงอยู่ 7 วัน
7-day retentionโดยรวมต่ำกว่า1-day retentionก็คือ มีจำนวนผู้เล่นน้อยกว่า (ทั้ง 2 กลุ่มประมาณ 19%) เมื่อเทียบกับการคงอยู่ 1 วันหลังจากติดตั้ง (ทั้ง 2 กลุ่มประมาณ 44%) — และก็หมายถึง 81% ของผู้เล่นไม่ได้เล่นเกมภายใน 7 วันหลังจากติดตั้ง 7-day retentionจะลดลงเล็กน้อยเมื่อ gate อยู่ที่เลเวล 40 (18.2%) เมื่อเทียบกับเมื่อ gate อยู่ที่เลเวล 30 (19.0%)- ความแตกต่างนี้ยังมากกว่า
1-day retentionซึ่งสันนิษฐานว่าเป็นเพราะผู้เล่นมีเวลาเข้าประตูแรกมากกว่า (เลเวล 30 เป็น gate แรก)
และเช่นเดียวกับก่อนหน้านี้ เราจะมาใช้ bootstrap เพื่อหาความแน่นอนของความแตกต่างระหว่างกลุ่ม AB
# boots Diff A-B group
boots_stat <- function(data, indices) {
# ดึงข้อมูล index ที่ Resample มา
d <- data[indices, ]
# คำนวณค่าเฉลี่ยของแต่ละกลุ่มและหาผลต่าง
mean_A <- d %>% filter(version == "gate_30") %>% pull(retention_7) %>% mean(na.rm = TRUE)
mean_B <- d %>% filter(version == "gate_40") %>% pull(retention_7) %>% mean(na.rm = TRUE)
return(((mean_B-mean_A)/mean_A)*100)
}
boot_ab <- boot(
data = df,
statistic = boots_stat,
R = 1000 # จำนวนครั้ง
)
boot_ab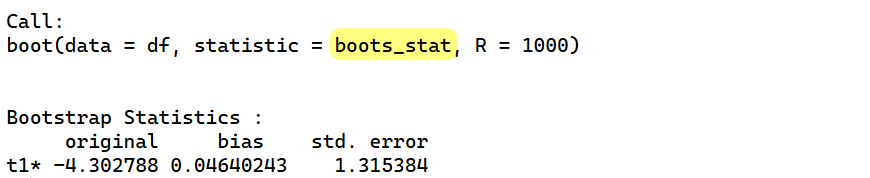
dif_ab <- as.data.frame(boot_ab[2])
ab_df <- dif_ab %>% select( diff_ab = t)
rm(dif_ab)
head(ab_df, 5)
mean(ab_df$diff_ab < 0)
# % per diff
ggplot(ab_df, aes(x = diff_ab)) +
geom_density(alpha = 0.5) + # Use transparency for better visualization
labs(title = "Density Plot of % diff_ab",
x = "Value",
y = "Density") +
theme_minimal()
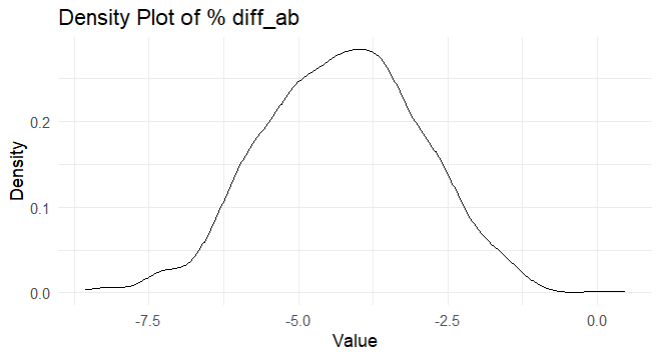
เราจะเห็นว่าเปอร์เซ็นต์ความแตกต่างที่เป็นไปได้ ส่วนใหญ่จะต่ำกว่า -2% ที่ 99% (0.998) แน่นอนว่าสนับสนุน gate ที่เลเวล 30 (gate_30) กว่ามากๆ
Conclusion
- ผลจาก bootstrap บอกเราว่าอัตราการคงอยู่ของผู้เล่น
7-day retentionจะสูงกว่าเมื่อ gate อยู่ที่เลเวล 30 เมื่อเทียบกับ gate อยู่ที่เลเวล 40 นั่นคือ: หากเราต้องการรักษาอัตราการคงอยู่ของผู้เล่นให้มาก เราไม่ควรย้าย gate จากเลเวล 30 ไปที่เลเวล 40 (หากผู้ให้บริการยังคงมีบริการแบบเดิมอยู่) - แน่นอนว่ายังมีตัวชี้วัดอื่นๆ ที่เราสามารถดูได้ เช่น จำนวนรอบเกมที่เล่น หรือจำนวนการซื้อไอเทมในเกมของกลุ่ม AB ทั้งสองกลุ่ม แต่อัตราการคงอยู่เป็นหนึ่งในตัวชี้วัดที่สำคัญที่สุด หากเราไม่สามารถรักษาฐานผู้เล่นไว้ได้ จำนวนเงินที่พวกเขาใช้ในเกมก็ไม่สำคัญ
- แล้วทำไมอัตราการคงอยู่จึงสูงกว่าเมื่อ gate ถูกวางไว้ก่อน(ที่เลเวล 30)? เราอาจคิดว่า: ยิ่งอุปสรรคอยู่ไกลเท่าไหร่ ผู้คนก็จะยิ่งมีส่วนร่วมกับเกมนานขึ้นเท่านั้น แต่ทางทฤษฎีการปรับตัวตามความสุข (hedonic adaptation) สามารถอธิบายเรื่องนี้ได้อย่างอีกแบบหนึ่ง
- การปรับตัวตามอารมณ์ (Hedonic Adaptation) คือแนวโน้มที่ผู้คนจะรู้สึกสนุกกับกิจกรรมต่างๆ น้อยลงเรื่อยๆ หากทำกิจกรรมนั้นอย่างต่อเนื่อง การบังคับให้ผู้เล่นหยุดพักเมื่อถึง gate ทางเข้าจะทำให้ความสนุกของเกมยาวนานขึ้น แต่เมื่อ gate ทางเข้าถูกเลื่อนไปถึงเลเวล 40 ผู้เล่นจึงมีแนวโน้มที่จะเลิกเล่นเกมเพราะเบื่อมากขึ้น






